Using the Sidebar Menu
October 5, 2020The early tutorials have shown you how to make forecasts using the
FORGE_FORECAST function. You can also make forecasts by using the sidebar;
this tutorial will show you how to do this and some of the extra features you
can use when making a forecast this way.
You can watch this video for a quick demo of how things work and bit of explanation. Or read on below…
The first thing you will have to do is open the sidebar if it isn’t open already.
After a short loading period you should see it appear on the right of your screen:
Read moreHow Good is my Forecast?
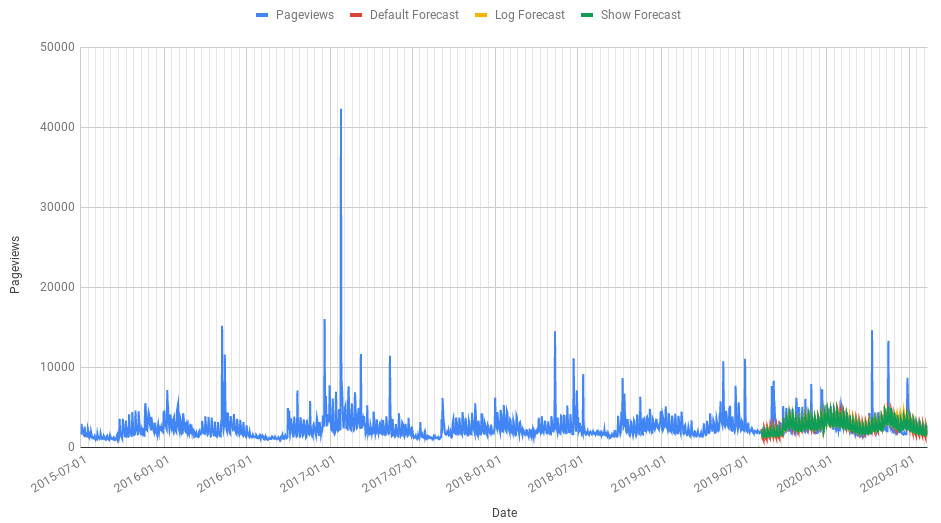
September 3, 2020If you have enough data then the Forecast Forge addon will estimate how accurate your forecast is likely to be.
How it works
We don’t know what will happen in the future so it is impossible to be certain how good or bad your forecast will be. But we can use the same forecasting algorithm to make a forecast for the recent past and then compare how accurate that forecast is against what actually happened.
For example, you might pretend you don’t know what happened between April 2019 and April 2020 (and I think we’d all like to imagine this didn’t happen at all!) and use the data from April 2017 to March 2019 to feed into the forecasting algorithm.
Then you can compare the results of this forecast with the actual data for 2019/20 to see how good the forecasting algorithm is at predicting with your data.
You have this data
2018 2019 2020
/----------/-----------/-----
|~~~~~~
And you want to forecast this
Use this data
2018 2019 2020
/----------/-----------/-----
|~~~~~~
To forecast thisMeasuring Error
The Forecast Forge addon shows you four different ways of measuring the error. They are each useful in different circumstances.
Every error metric is based on the daily errors; the difference between the actual value and the forecast value for each day in the forecast.
1. ME - Mean Error
Take all the error values and find the mean.
This is the simplest error metric but it doesn’t always tell you the full story because positive and negative errors (where the forecast over- and under-estimates) can cancel each other out.
The main thing the Mean Error tells you is whether the forecast tends to overestimate (positive error) or underestimate (negative error).
2. MAE - Mean Absolute Error
Take the absolute value of the errors (i.e. make them all positive) and then find the mean.
This fixes the problem with Mean Error described above.
3. RMSE - Root Mean Squared Error
Square all the error values, find the mean of this and then take the square root.
This is a very commonly used error metric in machine learning. I strongly suggest you try to minimise this error when working to improve your forecasts unless you have a very good reason not to.
However, this can be a bit harder to understand than the other error metrics so once you have your model figured out you can report MAE or MAPE to your clients who aren’t elbows deep in forecasting.
4. MAPE - Mean Absolute Percentage Error
Find the error values as a percentage, take the absolute value and then calculate the mean of this.
This is a very useful error metric because it is a percentage; it doesn’t matter what scale the values being forecast are.
For example, imagine I tell you that I’ve made a forecast for average order value (AOV) and
that my MAE is 15. Is this good or bad?
It is impossible to say without knowing more about the average order value. If
it is very high (e.g. over $200) then 15 is quite good. If it is very low
(e.g. $20) then 15 is very bad!
But if you have a MAPE of 10% then you don’t need to know how big or small the
AOV is to assess how much of a problem the error might be.
For more detail on running backtests manually or using other error metrics read the Backtesting Forecasts to Estimate Future Accuracy post.
I Think You’ll Find It’s a Bit More Complicated Than That
As with just about everything, it’s a bit more complicated than that!

Logit Transforms
August 21, 2020The Logit Transform is most useful when the metric you are forecasting has both a ceiling and a floor. For example a forecast for a conversion rate must be between 0% and 100%. Or, the number of users for a site must be between 0 and the total population of the world.
That last one is probably only a concern for Google and Facebook!
In Search you might use this if you have an idea of how many searches are going to be done through the year; the number of impressions you get can’t be higher than this number and it can’t be lower than 0. NB in this example the ceiling cap is variable; the number of searches isn’t the same every day.
For this example I will, again, show you something with Wikipedia pageview data.
This Google Sheet has three columns of data:
- The total number of pageviews for every page in the American politicians killed in duels category
- The number of pageviews for the Alexander Hamilton page
- The proportion of category pageviews which are on the Hamilton page
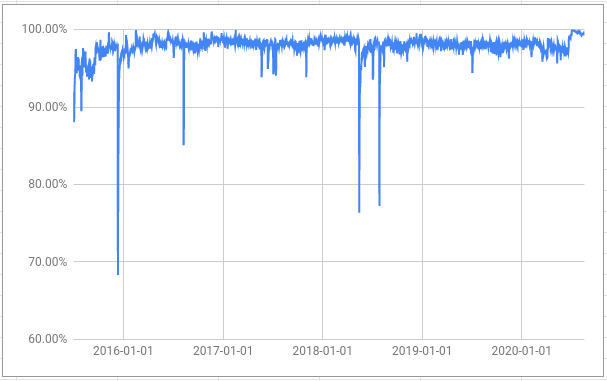
The proportion is what we are interested in here; we know that this can never be less than 0% or more than 100%.
Box-Cox Transforms
August 20, 2020Yesterday I updated the addon to include two new data transformations:
- The Box-Cox transformation
- The Logit transformation
You can read a little introduction on transforming data and why this is useful in the Improving Forecasts tutorial.
But why specifically are these transformations useful and when should you use them?
You can read about the Logit transform in another tutorial. Right now, here is the Box-Cox transform.
Box-Cox Transformation
You can follow along with this example in this Google Sheet which uses the pageviews of the wikipedia Easter article.
Drawing a histogram of the daily pageviews looks like this:
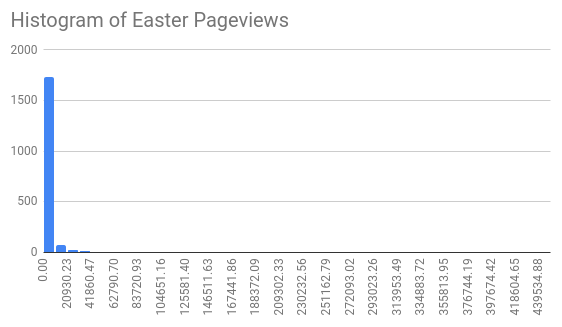
Almost all days have a small number of pageviews (the tall bar on the left) and then there are some that are way more popular (the invisibly small bars that extend to the right). This is common for highly seasonal data like this.
Read moreBacktesting Forecasts to Estimate Future Accuracy
August 17, 2020There are lots of things you can do when preparing a forecast but how do you know the things you should do?
You want the forecasting methods that will produce the best predictions about the future but, and this is the tricky part, you need to pick a method now; before you know anything about the future values.
One way to get more confidence that you are picking the best method is to “backtest” your methodology against historical data.
For example, you might pretend you don’t know what happened between April 2019 and April 2020 (and I think we’d all like to imagine this didn’t happen at all!) and use the data from April 2017 to March 2019 to feed into the forecasting algorithm.
Then you can compare the results of this forecast with the actual data for 2019/20 to see if the changes you are making to inputs or methodology are making the forecast better.
Use data from this period To predict here
________________________________________~~~~~~~~~~~~~
|------------|------------|------------|------------|--------????|?????????
2016 2017 2018 2019 2020 Then use the same
methodology herePicking an error metric
There are a few common ways of measuring how bad a forecast is. You need to match your error method with the goal of the forecast you are making and then you can work at improving things until you feel able to pick the forecast with the lowest error.
1. Mean error (ME)
For each day in the forecast, calculate the difference between the forecasted value and the actual value. Then find the mean of all these values.
If the value is positive then your forecast tends to underestimate and if it is negative it tends to overestimate the true values.
This error metric is rarely used by itself because you can have a forecast that is always a very long way from the true value but, as long as the positive and negative errors cancel out, the mean error can be very low. I’ve included it in this list only because it is the simplest error metric.
2. Mean absolute error (MAE)
This is very similar to the above except you use the absolute value to make all the daily errors positive before you find the mean. This fixes the problem of positive and negative errors balancing each other out and makes for a nice easy way of explaining how good or bad a forecast is.
3. Mean squared error (MSE)
Another way to transform the error values (also known as “residuals”) into a positive number is to square them rather than use the absolute value function.
Be aware than this means a few large errors can cause this metric to “blow up” in a way that MAE doesn’t.
| Day | Actual | Forecast |
|---|---|---|
| 2020-08-01 | 100 | 102 |
| 2020-08-02 | 95 | 97 |
| 2020-08-03 | 99 | 97 |
| 2020-08-04 | 80 | 69 |
| 2020-08-05 | 81 | 79 |
| 2020-08-06 | 98 | 101 |
| 2020-08-07 | 105 | 104 |
The MAE for this forecast is (2+2+11+2+3+1)/7 = 22/7 ~= pi
The MSE is (4+4+121+4+9+1)/7 = 143/7
The important thing to see here isn’t that the MSE is much bigger. The important
thing to notice is the huge difference in the proportion of the error that comes
from 2020-08-04; for the MSE 121 is sooooo much bigger than all the other
squared error values.
Mean squared error is much more sensitive to outliers than mean absolute error. A forecast that is mostly right but sometimes very wrong will score worse here than a forecast that is more consistently wrong.
MSE also has theoretical importance for two main reasons:
- In a lot of cases minimising MSE is equivalent to maximising the likelihood of a model with normally distributed residuals. Normally distributed residuals is a very common assumption across lots of data science.
- The error function is differentiable everywhere which is important for machine learning algorithms like gradient descent.
Neither of these things should concern you as users of the forecasting addon but they are important if you want to improve your general knowledge in this area.
4. Mean absolute percentage error (MAPE)
Imagine I tell you that I’ve made a forecast for average order value (AOV) and
that my MAE is 15. Is this good or bad?
It is impossible to say without knowing more about the average order value. If
it is very high (e.g. over $200) then 15 is quite good. If it is very low
(e.g. $20) then 15 is very bad!
Calculating a percentage error avoids this problem because the error is scaled with the value of the thing you are trying to forecast. A percentage is also much more commonly understood than an MSE value which helps when communicating with stakeholders who aren’t armpit deep in the details of forecasting.
However, if the real values vary over a wide range then MAPE can suffer from similar problems to MSE:
| Day | Actual | Forecast |
|---|---|---|
| 2020-08-01 | 100 | 101 |
| 2020-08-02 | 95 | 110 |
| 2020-08-03 | 99 | 90 |
| 2020-08-04 | 1 | 5 |
| 2020-08-05 | 81 | 79 |
| 2020-08-06 | 98 | 88 |
| 2020-08-07 | 105 | 94 |
The MAE for this forecasts is (1+15+9+4+2+10+11)/7 = 52/7 ~= 7.43
The MAPE is (1%+15.8%+9.1%+400%+2.5%+10.2%+10.5%)/7 = 446/7 ~= 63.8%
Because the value on 2020-08-04 is of a different magnitude than the rest it’s
contribution to the MAPE is disproportionately large even though the error is
only 4.
This won’t be a problem for you in real life unless you regularly see some values that are much smaller than the rest. This might happen in a rapidly growing business (the forecast would bias towards making better predictions at the start of the growth curve rather than further in the future) or if you are forecasting something that is rare except in a particular season.
5. Weighted variants of the above
All of the above methods can be adjusted to give more weight to errors at particular times of year.
For example, you might weight errors in Q4 more heavily because this is a particularly important time of year to get right.
6. Aggregate variants of the above
The forecasting addon produces daily forecasts but often you don’t care very much about the daily values; it is more important to get the weekly or monthly totals correct.
In this case, you can calculate the actual totals and the totals for the forecast and then use one of the above error metrics on them.
Normally an aggregate error metric will be lower/better than the daily because positive and negative errors will cancel each other out a bit.
Example
In this Google Sheet you can see an example of four different forecasts, each of which tries to accurately predict the number of pageviews of the Graham Norton wikipedia page.